机器学习

KNN

kNN 算法概述

KNN 可以说是最简单的分类算法之一，同时，它也是最常用的分类算法之一，注意 KNN 算法是有监督学习中的分类算法，它看起来和另一个机器学习算法 Kmeans 有点像（Kmeans 是无监督学习算法），但却是有本质区别的。那么什么是 KNN 算法呢，接下来我们就来介绍介绍吧。

算法介绍

KNN 的全称是 K Nearest Neighbors，意思是 K 个最近的邻居

K 个最近邻居，毫无疑问，K 的取值肯定是至关重要的。

KNN 的原理就是当预测一个新的值 x 的时候，根据它距离最近的 K 个点是什么类别来判断 x 属于哪个类别

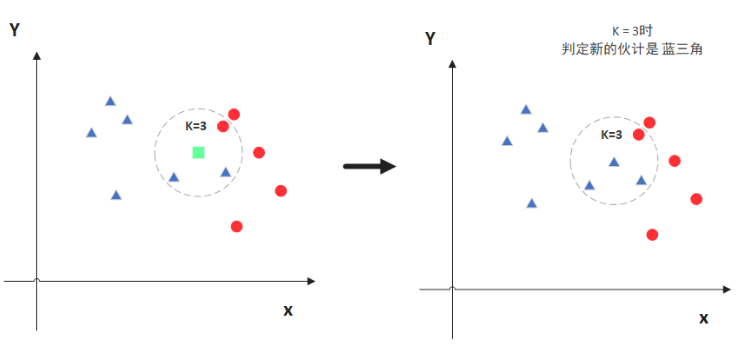
图中绿色的点就是我们要预测的那个点，假设 K=3。

那么 KNN 算法就会找到与它距离最近的三个点（这里用圆圈把它圈起来了），看看哪种类别多一些，比如这个例子中是蓝色三角形多一些，新来的绿色点就归类到蓝三角了。

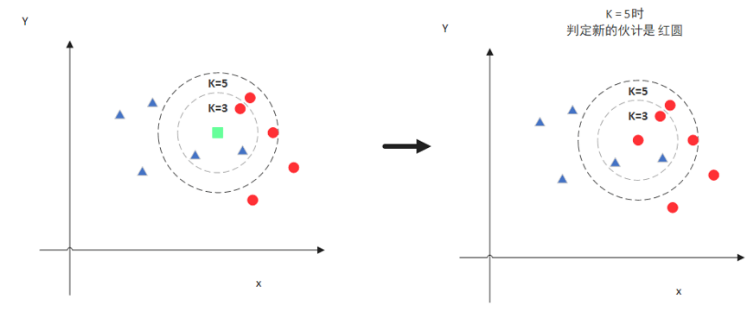
但是，当 K=5 的时候，判定就变成不一样了。这次变成红圆多一些，所以新来的绿点被归类成红圆。从这个例子中，我们就能看得出 K 的取值是很重要的。

明白了大概原理后，我们就来说一说细节的东西吧，主要有两个，K 值的选取和点距离的计算。

距离计算

要度量空间中点距离的话，有好几种度量方式，比如常见的曼哈顿距离计算，欧式距离计算等等。

不过通常 KNN 算法中使用的是欧式距离，这里只是简单说一下，拿二维平面为例，，二维空间两个点的欧式距离计算公式如下：

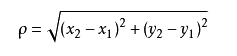
这个高中应该就有接触到的了，其实就是计算（x1,y1）和（x2,y2）的距离。拓展到多维空间，则公式变成这样：

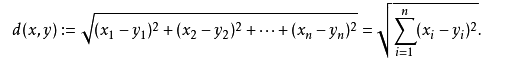
K 值选择

通过上面那张图我们知道 K 的取值比较重要，那么该如何确定 K 取多少值好呢？答案是通过交叉验证（将样本数据按照一定比例，拆分出训练用的数据和验证用的数据，比如 6：4 拆分出部分训练数据和验证数据），从选取一个较小的 K 值开始，不断增加 K 的值，然后计算验证集合的方差，最终找到一个比较合适的 K 值。

通过交叉验证计算方差后你大致会得到下面这样的图：

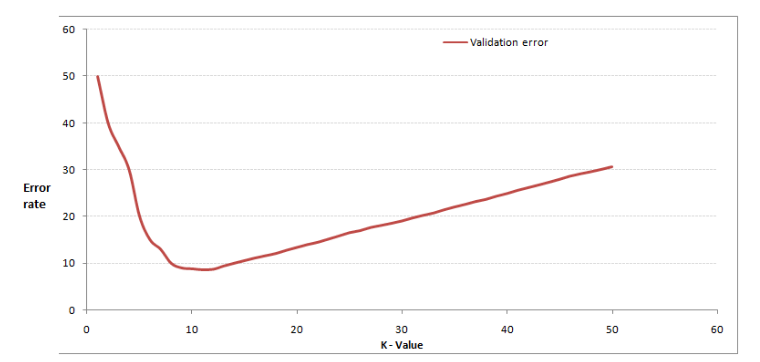
当你增大 k 的时候，一般错误率会先降低，因为有周围更多的样本可以借鉴了，分类效果会变好。但注意，和 K-means 不一样，当 K 值更大的时候，错误率会更高。这也很好理解，比如说你一共就 35 个样本，当你 K 增大到 30 的时候，KNN 基本上就没意义了。

所以选择 K 点的时候可以选择一个较大的临界 K 点，当它继续增大或减小的时候，错误率都会上升，比如图中的 K=10。具体如何得出 K 最佳值的代码，下一节的代码实例中会介绍。

KNN 特点

KNN 是一种非参的，惰性的算法模型。什么是非参，什么是惰性呢？

非参的意思并不是说这个算法不需要参数，而是意味着这个模型不会对数据做出任何的假设，与之相对的是线性回归（我们总会假设线性回归是一条直线）。也就是说 KNN 建立的模型结构是根据数据来决定的，这也比较符合现实的情况，毕竟在现实中的情况往往与理论上的假设是不相符的。

惰性又是什么意思呢？想想看，同样是分类算法，逻辑回归需要先对数据进行大量训练（tranning），最后才会得到一个算法模型。而 KNN 算法却不需要，它没有明确的训练数据的过程，或者说这个过程很快。

KNN 算法的优势和劣势

了解 KNN 算法的优势和劣势，可以帮助我们在选择学习算法的时候做出更加明智的决定。那我们就来看看 KNN 算法都有哪些优势以及其缺陷所在！

KNN 算法优点

1. 简单易用，相比其他算法，KNN 算是比较简洁明了的算法。即使没有很高的数学基础也能搞清楚它的原理。
2. 模型训练时间快，上面说到 KNN 算法是惰性的，这里也就不再过多讲述。
3. 预测效果好。
4. 对异常值不敏感

KNN 算法缺点

1. 对内存要求较高，因为该算法存储了所有训练数据
2. 预测阶段可能很慢
3. 对不相关的功能和数据规模敏感

使用时机

当需要使用分类算法，且数据比较大的时候就可以尝试使用 KNN 算法进行分类了。

Skelarn KNN 参数概述

要使用 sklearnKNN 算法进行分类，我们需要先了解 sklearnKNN 算法的一些基本参数

def KNeighborsClassifier(n_neighbors = 5,
                       weights='uniform',
                       algorithm = '',
                       leaf_size = '30',
                       p = 2,
                       metric = 'minkowski',
                       metric_params = None,
                       n_jobs = None
                       )

- n_neighbors：这个值就是指 KNN 中的 “K”了。前面说到过，通过调整 K 值，算法会有不同的效果。
- weights（权重）：最普遍的 KNN 算法无论距离如何，权重都一样，但有时候我们想搞点特殊化，比如距离更近的点让它更加重要。这时候就需要 weight 这个参数了，这个参数有三个可选参数的值，决定了如何分配权重。参数选项如下：
        • 'uniform'：不管远近权重都一样，就是最普通的 KNN 算法的形式。
        • 'distance'：权重和距离成反比，距离预测目标越近具有越高的权重。
        • 自定义函数：自定义一个函数，根据输入的坐标值返回对应的权重，达到自定义权重的目的。
- algorithm：在 sklearn 中，要构建 KNN 模型有三种构建方式，1. 暴力法，就是直接计算距离存储比较的那种放松。2. 使用 kd 树构建 KNN 模型 3. 使用球树构建。 其中暴力法适合数据较小的方式，否则效率会比较低。如果数据量比较大一般会选择用 KD 树构建 KNN 模型，而当 KD 树也比较慢的时候，则可以试试球树来构建 KNN。参数选项如下：
        • 'brute' ：蛮力实现
        • 'kd_tree'：KD 树实现 KNN
        • 'ball_tree'：球树实现 KNN
        • 'auto'： 默认参数，自动选择合适的方法构建模型
不过当数据较小或比较稀疏时，无论选择哪个最后都会使用 'brute'

- leaf_size：如果是选择蛮力实现，那么这个值是可以忽略的，当使用KD树或球树，它就是是停止建子树的叶子节点数量的阈值。默认30，但如果数据量增多这个参数需要增大，否则速度过慢不说，还容易过拟合。
- p：和metric结合使用的，当metric参数是"minkowski"的时候，p=1为曼哈顿距离， p=2为欧式距离。默认为p=2。
- metric：指定距离度量方法，一般都是使用欧式距离。
        • 'euclidean' ：欧式距离
        • 'manhattan'：曼哈顿距离
        • 'chebyshev'：切比雪夫距离
        • 'minkowski'： 闵可夫斯基距离，默认参数
- n_jobs：指定多少个CPU进行运算，默认是-1，也就是全部都算。

KNN 代码实例

KNN 算法算是机器学习里面最简单的算法之一了，我们来 sklearn 官方给出的例子，来看看 KNN 应该怎样使用吧：

数据集使用的是著名的鸢尾花数据集，用 KNN 来对它做分类。我们先看看鸢尾花长的啥样。

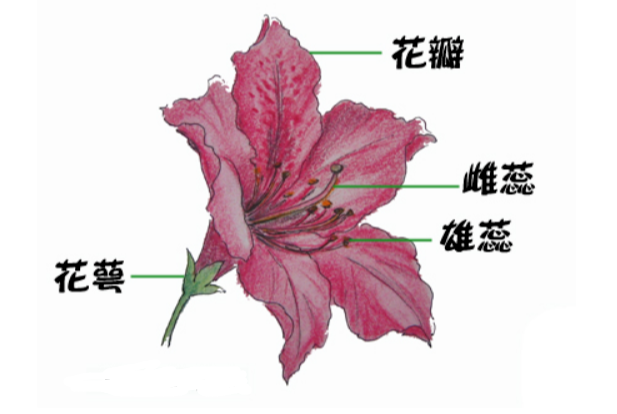
面这个就是鸢尾花了，这个鸢尾花数据集主要包含了鸢尾花的花萼长度，花萼宽度，花瓣长度，花瓣宽度 4 个属性（特征），以及鸢尾花卉属于『Setosa，Versicolour，Virginica』三个种类中的哪一类（这三种都长什么样我也不知道）。

在使用 KNN 算法之前，我们要先决定 K 的值是多少，要选出最优的 K 值，可以使用 sklearn 中的交叉验证方法，代码如下：

from sklearn.datasets import load_iris
from sklearn.model_selection  import cross_val_score
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier

#读取鸢尾花数据集
iris = load_iris()
x = iris.data
y = iris.target
k_range = range(1, 31)
k_error = []
#循环，取k=1到k=31，查看误差效果
for k in k_range:
    knn = KNeighborsClassifier(n_neighbors=k)
    #cv参数决定数据集划分比例，这里是按照5:1划分训练集和测试集
    scores = cross_val_score(knn, x, y)
    k_error.append(1 - scores.mean())

#画图，x轴为k值，y值为误差值
plt.plot(k_range, k_error)
plt.xlabel('Value of K for KNN')
plt.ylabel('Error')
plt.show()

运行后，我们可以得到下面这样的图：

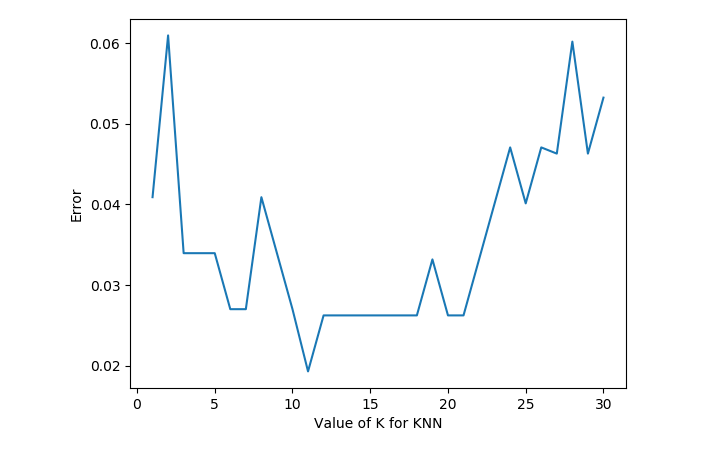
有了这张图，我们就能明显看出 K 值取多少的时候误差最小，这里明显是 K=11 最好。当然在实际问题中，如果数据集比较大，那为减少训练时间，K 的取值范围可以缩小。

有了 K 值我们就能运行 KNN 算法了，具体代码如下：

#鸢尾花
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris

X_train, X_test, y_train, y_test = train_test_split(x , y, test_size=0.25,random_state = 0)

knn = neighbors.KNeighborsClassifier(n_neighbors=11)
knn.fit(X_train, y_train)

print('模型评分：{:.2f}'.format(knn.score(X_test, y_test)))
print('模型评分2：{:.2f}'.format(knn.score(X_train, y_train)))

贝叶斯算法

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法。

贝叶斯定理

贝叶斯定理告诉我们如何交换条件概率中的条件与结果,

即如果已知P( X | H ),要求P( H | X ),那么可以使用下面的计算方法:

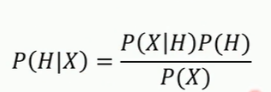
P( H | X )给定观测数据样本X ,假设H是成立的概率

比如X是一份具有特定特征的邮件, H是垃圾邮件。它里面包含很多的单词(特征) , 然后我们判断这封邮件属于垃圾邮件的概率是多少。

P( H | X)是后验概率。比如一份特定邮件中,是垃圾邮件的概率。
P(H)是H的先验概率。比如总体邮件中垃圾邮件的概率。
P(X )是X的先验概率。比如总体邮件中带有特定特征的邮件概率。

或者换个表达方式:

可以通过抽样来计算先验概率。抽样的数量越大,得到的结果越接近于真实的概率分布-大数定理。

举例:

朴素贝叶斯算法

朴素贝叶斯是贝叶斯决策理论的一部分。之所以称之为“朴素”，是因为整个形式化过程只做最原始、最简单的假设。

下面我先给出例子。

给定数据如下：

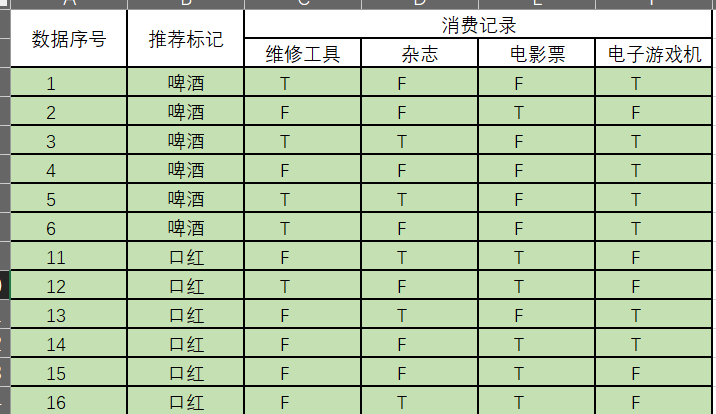
现在给我们的问题是，如果想给一个人推送消息,他的消费记录分别有维修工具,杂志,电影票,电子游戏机, 请你判断一下一个上述所有东西都买的人该给他推送啤酒还是口红

这是一个典型的分类问题，转为数学问题就是比较p(啤酒|(维修工具、杂志、电影票、电子游戏机))与p(口红|(维修工具、杂志、电影票、电子游戏机))的概率，谁的概率大，我就能给口红或者啤酒的答案！

这里我们联系到朴素贝叶斯公式：

我们需要求p(啤酒 | 维修工具、杂志、电影票、电子游戏机),这是我们不知道的，但是通过朴素贝叶斯公式可以转化为好求的三个量，p(维修工具、杂志、电影票、电子游戏机 | 啤酒)、p(维修工具、杂志、电影票、电子游戏机)、p(啤酒)（至于为什么能求，后面会讲，那么就太好了，将待求的量转化为其它可求的值，这就相当于解决了我们的问题！）

朴素贝叶斯算法的朴素一词解释

那么这三个量是如何求得？

是根据已知训练数据统计得来，下面详细给出该例子的求解过程。

回忆一下我们要求的公式如下：

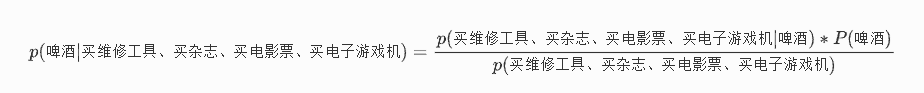
那么我只要求得p(买维修工具、买杂志、买电影票、买电子游戏机 | 啤酒)、p(买维修工具、买杂志、买电影票、买电子游戏机)、p(啤酒)即可, 下面我分别求出这几个概率, 最后一比,就得到最终结果

p(买维修工具、买杂志、买电影票、买电子游戏机 | 啤酒) = p(买维修工具 | 啤酒) * p(买杂志 | 啤酒) * p(买电影票 | 啤酒) * p(买电子游戏机 | 啤酒)

分别统计后面几个概率，也就得到了左边的概率！

等等，为什么这个成立呢？学过概率论的同学可能有感觉了，这个等式成立的条件需要特征之间相互独立吧！

对的！这也就是为什么朴素贝叶斯分类有朴素一词的来源，朴素贝叶斯算法是假设各个特征之间相互独立，那么这个等式就成立了！

但是为什么需要假设特征之间相互独立呢？

我们这么想，假如没有这个假设，那么我们对右边这些概率的估计其实是不可做的，这么说，我们这个例子有4个特征，其中维修工具包括{扳手，榔头}，杂志包括{体育，娱乐，花边}，电影票包括{流浪地球2，满江红，中国乒乓}，电子游戏机包括{Xbox，Ps5}，那么四个特征的联合概率分布总共是4维空间，总个数为2*3*3*2=36个。

24个，计算机扫描统计还可以，但是现实生活中，往往有非常多的特征，每一个特征的取值也是非常之多，那么通过统计来估计后面概率的值，变得几乎不可做，这也是为什么需要假设特征之间独立的原因。

假如我们没有假设特征之间相互独立，那么我们统计的时候，就需要在整个特征空间中去找，比如统计p(买维修工具、买杂志、买电影票、买电子游戏机 | 啤酒)

我们就需要在啤酒的条件下，去找四种特征全满足分别是买维修工具，买杂志，买电影票，买电子游戏机人的个数，这样的话，由于数据的稀疏性，很容易统计到0的情况。 这样是不合适的。

根据上面俩个原因，朴素贝叶斯法对条件概率分布做了条件独立性的假设，由于这是一个较强的假设，朴素贝叶斯也由此得名！这一假设使得朴素贝叶斯法变得简单，但有时会牺牲一定的分类准确率。

好的，上面我解释了为什么可以拆成分开连乘形式。那么下面我们就开始求解！

我们将上面公式整理一下如下：

下面我将一个一个的进行统计计算（在数据量很大的时候，根据中心极限定理，频率是等于概率的，这里只是一个例子，所以我就进行统计即可）。

p(啤酒) = ?

首先我们整理训练数据中，啤酒的样本数如下：

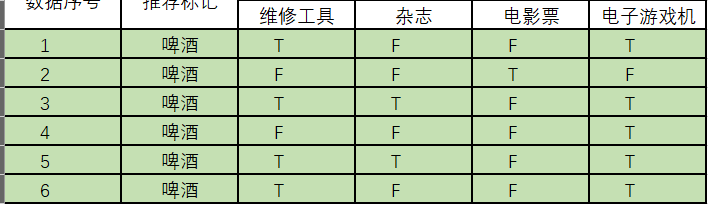
则p(啤酒) = 6 / 12 (总样本数) = 1/2

统计满足样本数

p(买维修工具 | 啤酒) = 4 / 6 = 2 / 3

p(买杂志 | 啤酒) = 2 / 6 = 1 / 3

p(买电影票| 啤酒) = 1 / 6

p(买电子游戏机 | 啤酒) = 5 / 6

下面开始求分母，p(买维修工具)，p（买杂志），p（买电影票），p（买电子游戏机）

统计样本如下：

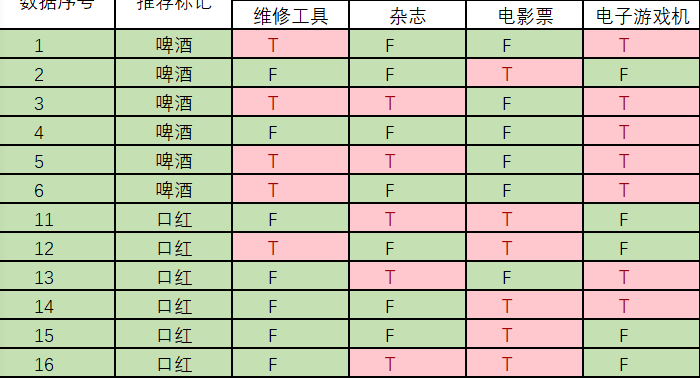
买维修工具统计如上红色所示，占5个，那么p(买维修工具) = 5 /12

买杂志统计如上红色所示，占5个，那么p(买杂志) = 5 /12

买电影票统计如上红色所示，占6个，那么p(买杂志) = 6 /12 = 1 / 2

买电子游戏机统计如上红色所示，占7个，那么p(买杂志) = 7 /12

到这里，要求p(买维修工具、买杂志、买电影票、买电子游戏机 | 啤酒)的所需项全部求出来了，下面带入进去即可，

= ((2 / 3 * 1 / 3 * 1 / 6 * 5 / 6 )* 1 / 2) / (5 / 12 * 5 / 12 * 1 / 2 * 7 / 12)

下面我们根据同样的方法来求p(买维修工具、买杂志、买电影票、买电子游戏机 | 口红)，完全一样的做法，为了方便理解，我这里也走一遍帮助理解。首先公式如下：

这里与上面公式中，分母是一样的，于是我们分母不需要重新统计计算！

下面我也一个一个来进行统计计算，这里与上面公式中，分母是一样的，于是我们分母不需要重新统计计算！

p(口红) = 6 / 12 = 1 / 2

p(买维修工具|口红) = ？统计满足条件的样本如下（红色为满足条件）：

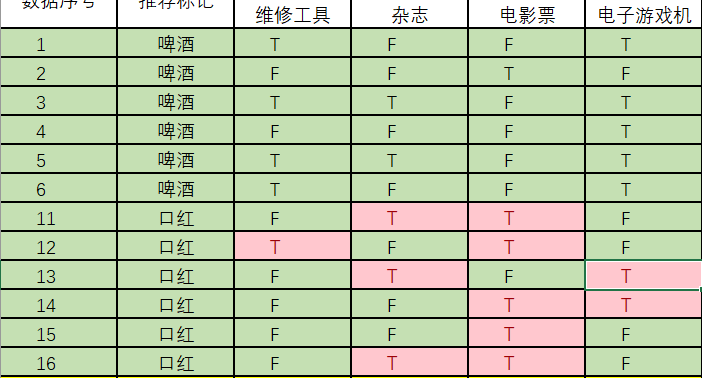
p(买维修工具|口红) = 1 / 6

p(买杂志|口红) = 3 / 6 = 1 / 2

p(买电影票|口红) = 5 / 6

p(电子游戏机|口红) = 2 / 6 = 1 / 3

那么根据公式：

p(买维修工具、买杂志、买电影票、买电子游戏机 | 口红) =

((1 / 6 * 1 / 2 * 5 / 6 * 1 / 3) * 1 / 2 ) / (5 / 12 * 5 / 12 * 1 / 2 * 7 / 12)

两者分母相同而且 p(口红)、p（啤酒）概率相同， 只需要比较一部分分子

很显然(2 / 3 * 1 / 3 * 1 / 6 * 5 / 6) > (1 / 6 * 1 / 2 * 5 / 6 * 1 / 3)

所以我们根据朴素贝叶斯算法可以给所有东西都买的人推送啤酒

题目换一下

同理

把买维修工具概率改为不买维修工具概率

求得p(不买维修工具 | 口红) * p(买杂志 | 口红) * p(买电影票 | 口红) * p(买电子游戏机 | 口红)

p(不买维修工具 | 啤酒) * p(买杂志 | 啤酒) * p(买电影票 | 啤酒) * p(买电子游戏机 | 啤酒)

比较两者概率

朴素贝叶斯分类的优缺点

优点：

（1） 算法逻辑简单,易于实现

（2）分类过程中时空开销小

缺点：

理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。

而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

拉普拉斯平滑系数

受训练数据集规模的限制，某个属性的取值可能在训练集中从未与某个类同时出现，这就可能导致属性条件概率为0，些时直接使用朴素贝叶斯分类就会导致错误的结论。

拉普拉斯平滑就是计算类先验概率和属性条件概率时，在分子上添加一个较小的修正量，在分母上则添加这个修正量与分类数目的乘积，避免了零概率对分类结果的影响。

操作

在计算时分子递增 1,而分母加上训练集总的分数类

这样就保证在偏差不大的情况下去除了0值的问题

朴素贝叶斯算法的不同方法

• 贝努利朴素贝叶斯
• 高斯贝叶斯
• 多项式朴素贝叶斯

伯努利朴素贝叶斯（Bernoulli Naive Bayes）

这种方法适用于符合伯努利分布的数据集

伯努利分布也被称作”二项分布”或者”0 - 1分布”

抛硬币只有两种结果,符合伯努利分布, 这种情况下适用伯努利

如果遇到更加复杂的数据集就不适用了

案例:

#sklearn.datasets.make_blobs () 是用于创建多类单标签数据集的函数，它为每个类分配一个或多个正态分布的点集。
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
X, y = make_blobs(n_samples = 500, centers = 5, random_state = 8)#生成一个5分类数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 8)
nb = BernoulliNB()#贝努利贝叶斯
nb.fit(X_train, y_train)#训练
print('模型得分:{:.3f}'.format(nb.score(X_test, y_test)))#得分

模型得分:0.544

我们会发现伯努利朴素贝叶斯在5个分类上的分类结果就不是很好

高斯朴素贝叶斯(Gaussian naive bayes)

顾名思义是假设样本的特征符合高斯分布或者正态分布所用的算法

from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(X_train, y_train)
print('模型得分:{:.3f}'.format(gnb.score(X_test, y_test)))#得分

模型得分:0.968

高斯朴素贝叶斯可以胜任大部分的分类任务

因为在自然科学和社会科学领域有大量现象都是呈现正态分布的

多项式朴素贝叶斯

用于拟合多项式分布的数据集

例如掷骰子,每次掷一次会得到 1~6中的一个数,如果掷n次, 1~6每个数出现的次数分布情况,就是一个多项式分布

from sklearn.naive_bayes import MultinomialNB
from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler()#把数据变为非负值
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)

mnb = MultinomialNB()
mnb.fit(X_train_scaled, y_train)
print('模型得分:{:.3f}'.format(mnb.score(X_test_scaled, y_test)))#得分

模型得分:0.320

MinMaxScaler

MinMaxScaler本质上就是归一化

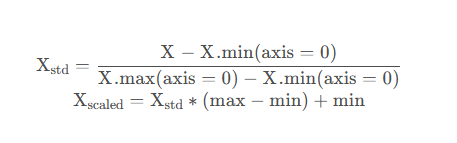
用朴实的语言描述一下上面公式所做的事：

1. 第一步求每个列中元素到最小值距离占该列最大值和最小值距离的比例，这实际上已经是将数据放缩到了[0,1]区间上
2. 第二步将标准化的数据映射到给定的[min,max]区间

给个例子

• X: 要归一化的数据，通常是二维矩阵

• [[4, 2, 3],[1, 5, 6]]

• X.min(axis=0)：每列中的最小值组成的行向量，如上面的例子中应该是[1,2,3]

• X.max(axis=0)：每列中的最大值组成的行向量，如上面的例子中应该是[4,5,6]

• max: 要映射到的区间最大值，默认是1

• min：要映射到的区间最小值，默认是0

• Xstd : 标准化结果

• Xscaled : 归一化结果

归一化实现

from sklearn.preprocessing import MinMaxScaler
import numpy as np

data = np.array([[4,2,3],
                [1,5,6]])

# 手动归一化
feature_range = [0,1]  # 要映射的区间
print(data.min(axis=0))
print(data.max(axis=0))
x_std = (data-data.min(axis=0))/(data.max(axis=0)-data.min(axis=0))
x_scaled = x_std*(feature_range[1]-feature_range[0]) + feature_range[0]
print('手动归一化结果：\n{}'.format(x_scaled))

# 自动归一化
scaler = MinMaxScaler()
print('自动归一化结果:\n{}'.format(scaler.fit_transform(data)))

手动归一化结果:
[[1, 0, 0],
[0, 1, 1]]
自动归一化结果:
[[1, 0, 0],
[0, 1, 1]]

再简要说一下sklearn.preprocessing.MinMaxScaler的用法

1. 初始化一个MinMaxScaler对象：scaler = MinMaxScaler()
2. 拟合并转换数据，本质上就是先求最大最小值，然后对数据按照公式计算：scaler.fit_transform(data)

MinMaxScaler本质上是将数据点映射到了[0,1]区间（默认），但实际使用的的时候也不一定是到[0,1]，你也可以指定参数feature_range，映射到其他区间。

scaler2 = MinMaxScaler(feature_range=[1,2])
print('自动归一化结果:\n{}'.format(scaler2.fit_transform(data)))

自动归一化结果:
[[2, 1, 1],
[1, 2, 2]]

总结

• 高斯朴素贝叶斯适用于特征呈正态分布的，
• 多项式贝叶斯适用于特征是多项式分布的，
• 伯努利贝叶斯适用于二项分布。