排序简介

「排序算法 Sorting Algorithm」使得列表中的所有元素按照从小到大的顺序排列。

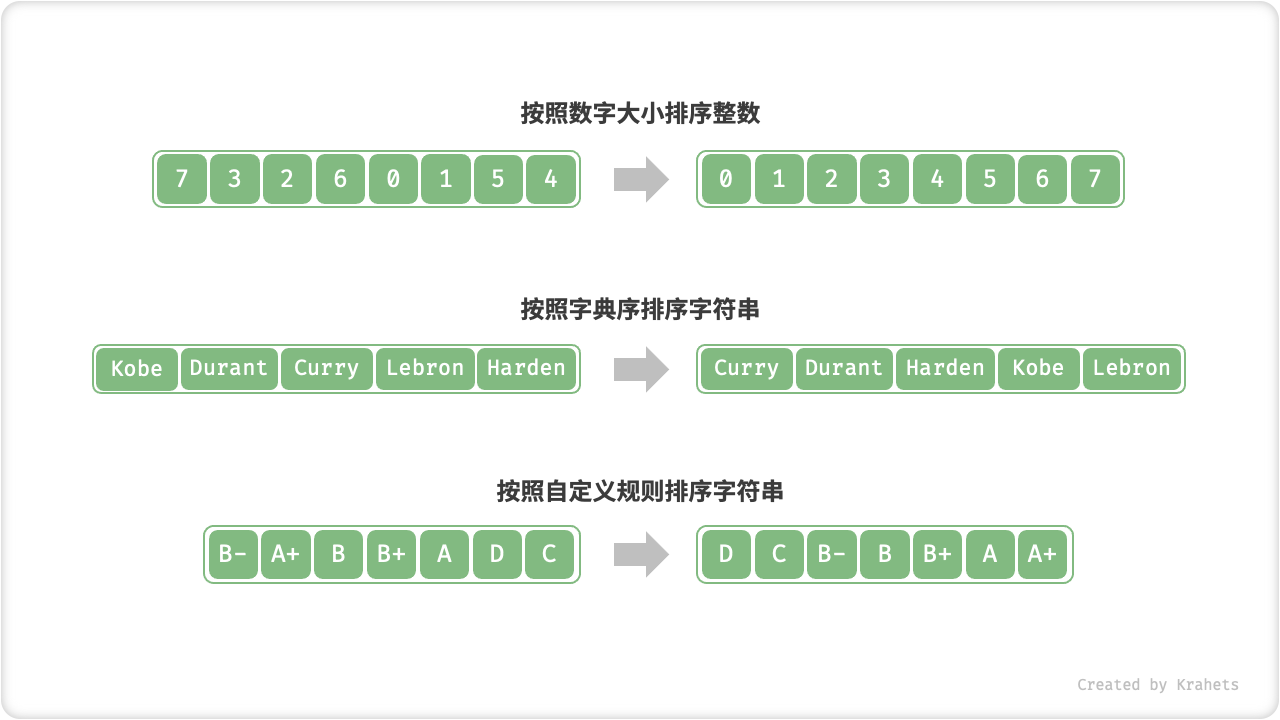
待排序的列表的 元素类型 可以是整数、浮点数、字符、或字符串；
排序算法可以根据需要设定 判断规则，例如数字大小、字符 ASCII 码顺序、自定义规则；

排序中的不同元素类型和判断规则

评价维度

排序算法主要可根据 稳定性、就地性、自适应性、比较类 来分类。

稳定性

「稳定排序」在完成排序后，不改变 相等元素在数组中的相对顺序。
「非稳定排序」在完成排序后，相等元素在数组中的相对位置 可能被改变。

假设我们有一个存储学生信息的表格，第 1, 2 列分别是姓名和年龄。那么在以下示例中，「非稳定排序」会导致输入数据的有序性丢失。因此「稳定排序」是很好的特性，在多级排序中是必须的。

# 输入数据是按照姓名排序好的
# (name, age)
  ('A', 19)
  ('B', 18)
  ('C', 21)
  ('D', 19)
  ('E', 23)

# 假设使用非稳定排序算法按年龄排序列表，
# 结果中 ('D', 19) 和 ('A', 19) 的相对位置改变，
# 输入数据按姓名排序的性质丢失
  ('B', 18)
  ('D', 19)
  ('A', 19)
  ('C', 21)
  ('E', 23)

就地性

「原地排序」无需辅助数据，不使用额外空间；
「非原地排序」需要借助辅助数据，使用额外空间；

「原地排序」不使用额外空间，可以节约内存；并且一般情况下，由于数据操作减少，原地排序的运行效率也更高。

自适应性

「自适应排序」的时间复杂度受输入数据影响，即最佳 / 最差 / 平均时间复杂度不相等。
「非自适应排序」的时间复杂度恒定，与输入数据无关。

我们希望 最差 = 平均，即不希望排序算法的运行效率在某些输入数据下发生劣化。

比较类

「比较类排序」基于元素之间的比较算子（小于、相等、大于）来决定元素的相对顺序。
「非比较类排序」不基于元素之间的比较算子来决定元素的相对顺序。

「比较类排序」的时间复杂度最优为 (O(n \log n)) ；而「非比较类排序」可以达到 (O(n)) 的时间复杂度，但通用性较差。

理想排序算法

运行快，即时间复杂度低；
稳定排序，即排序后相等元素的相对位置不变化；
原地排序，即运行中不使用额外的辅助空间；
正向自适应性，即算法的运行效率不会在某些输入数据下发生劣化；

然而，没有排序算法同时具备以上所有特性。排序算法的选型使用取决于具体的列表类型、列表长度、元素分布等因素。

冒泡排序

「冒泡排序 Bubble Sort」是一种最基础的排序算法，非常适合作为第一个学习的排序算法。顾名思义，「冒泡」是该算法的核心操作。

为什么叫”冒泡”

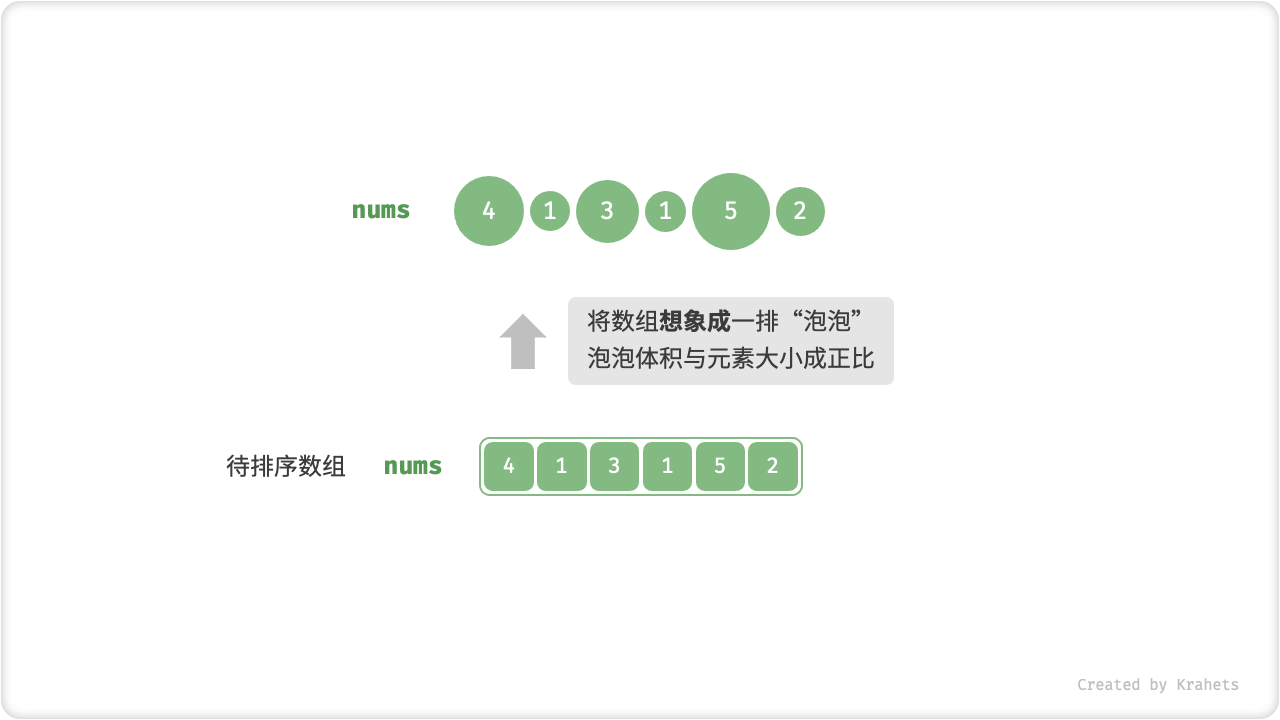
在水中，越大的泡泡浮力越大，所以最大的泡泡会最先浮到水面。

「冒泡」操作则是在模拟上述过程，具体做法为：从数组最左端开始向右遍历，依次对比相邻元素大小，若 左元素 > 右元素 则将它俩交换，最终可将最大元素移动至数组最右端。

完成此次冒泡操作后，数组最大元素已在正确位置，接下来只需排序剩余 (n - 1) 个元素。

冒泡操作

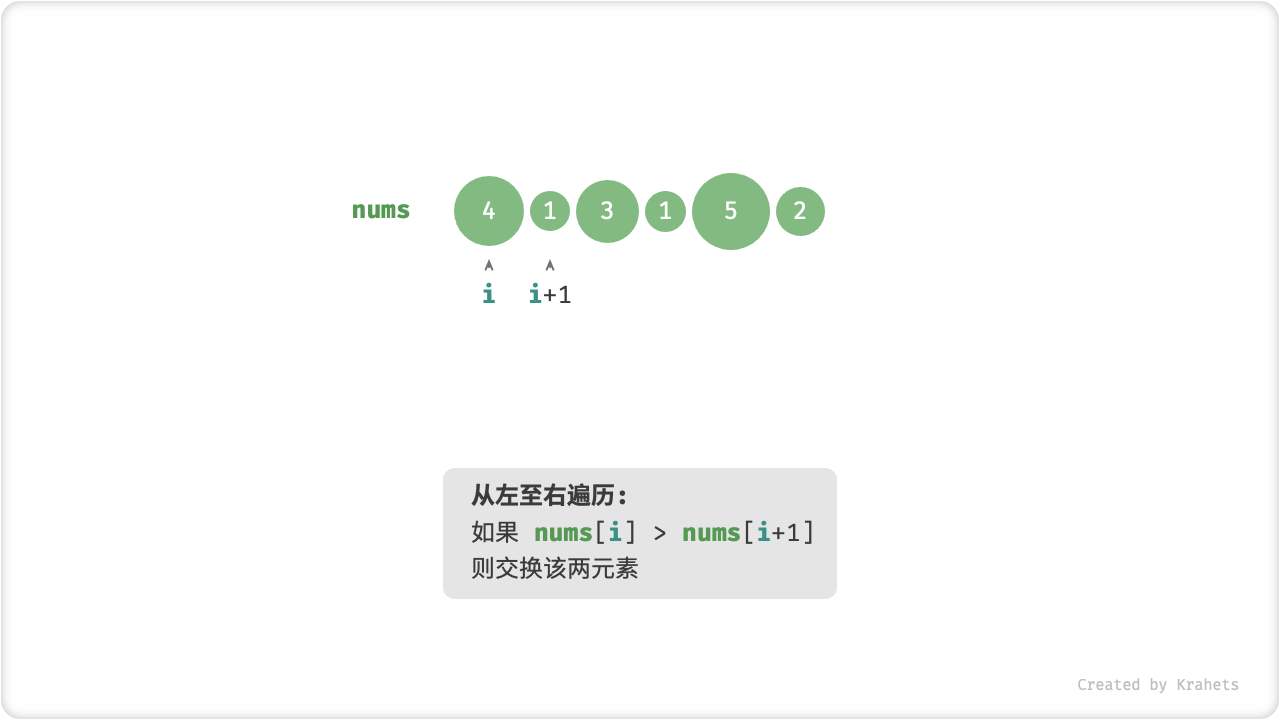
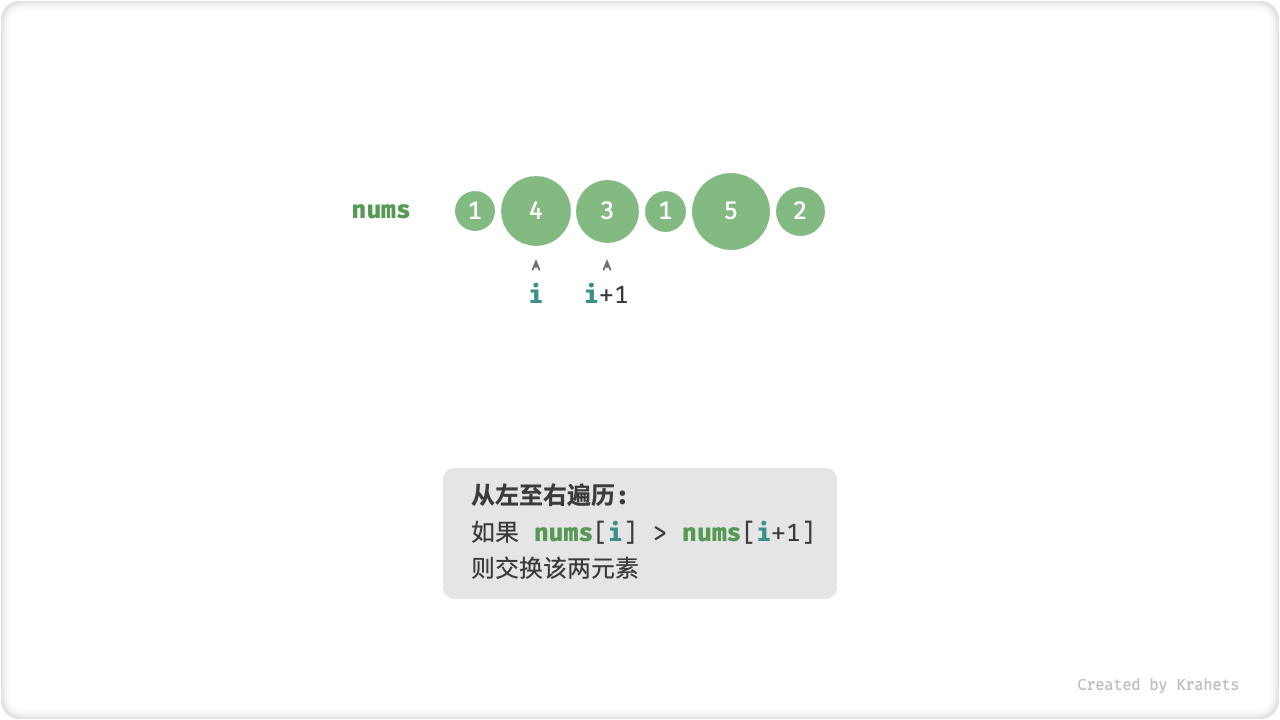
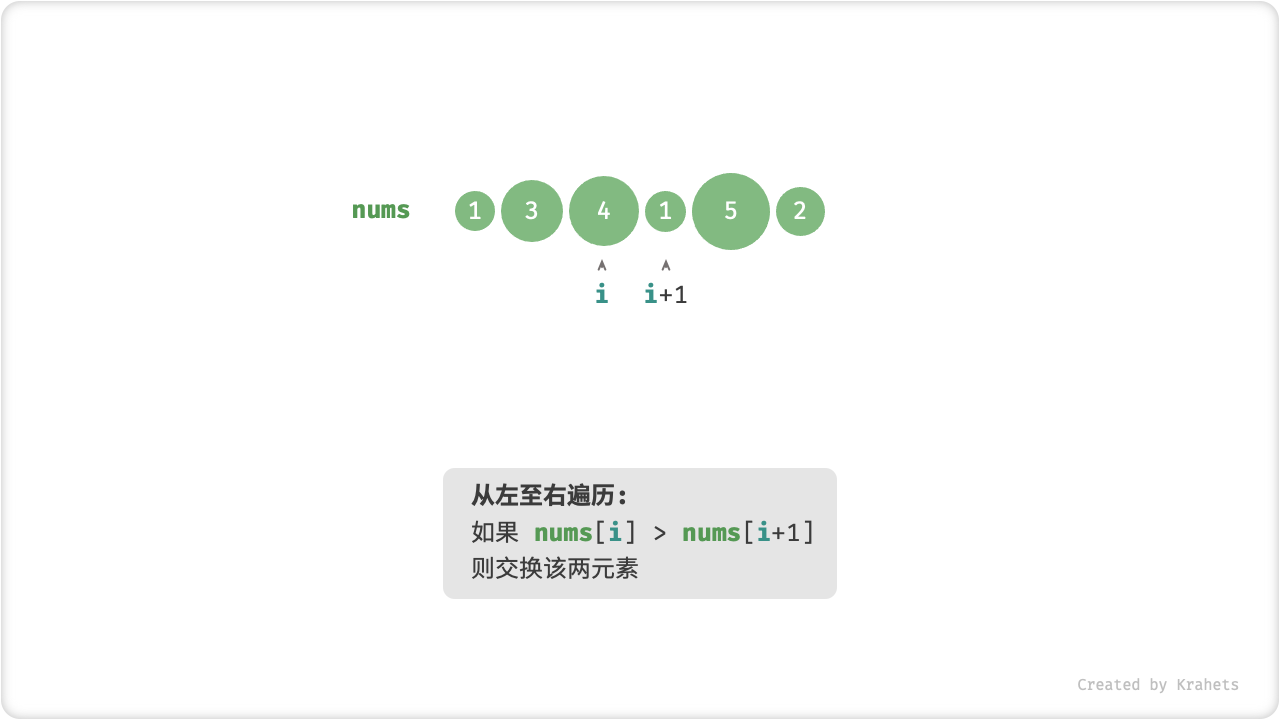
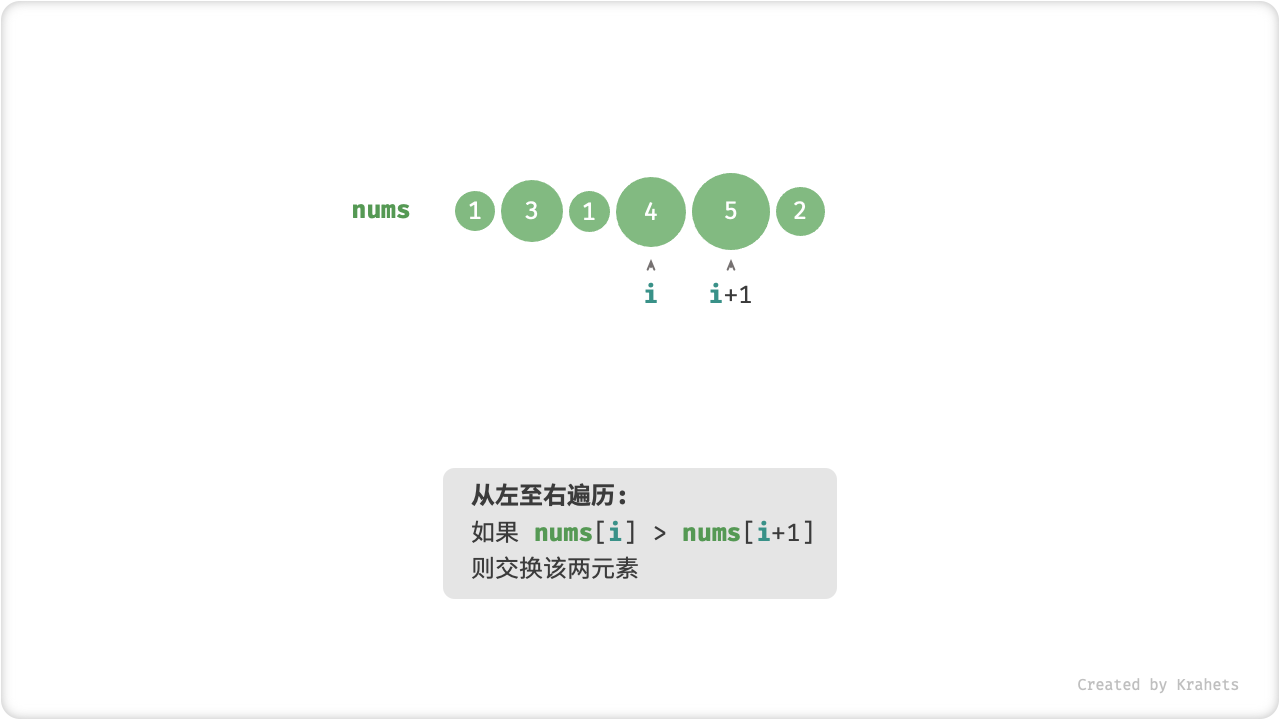
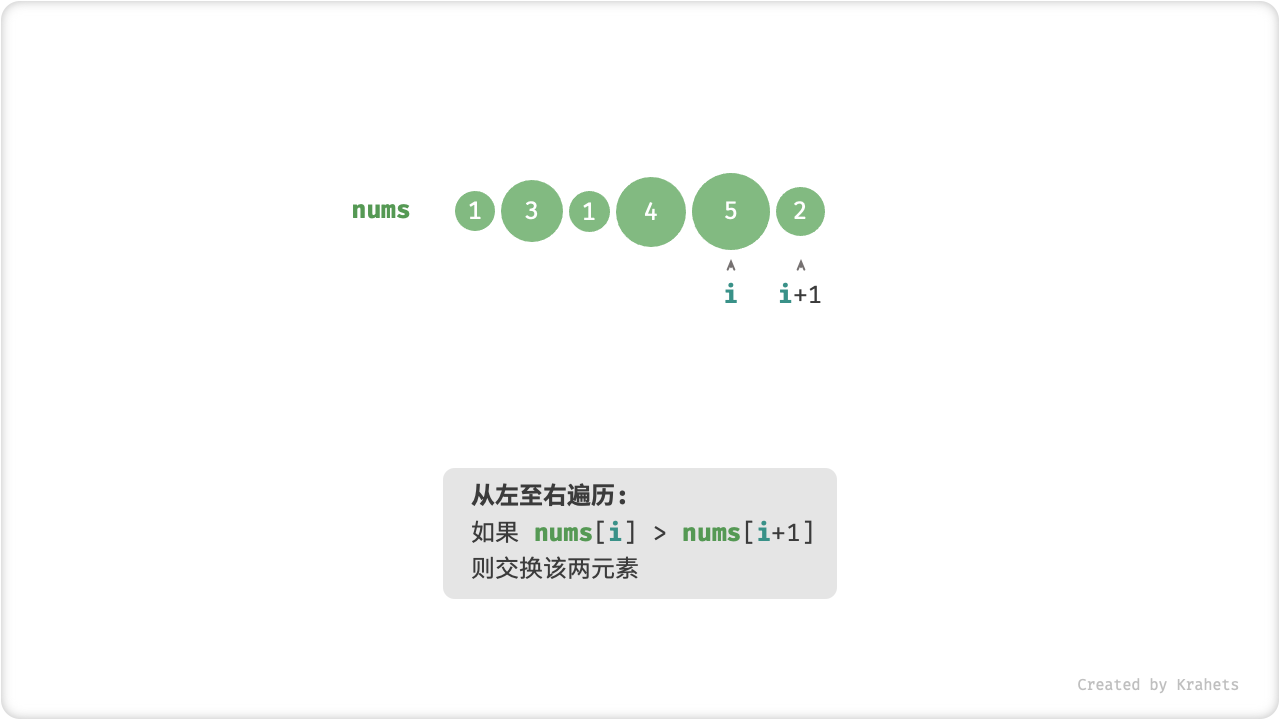
算法流程

设数组长度为 (n) ，完成第一轮「冒泡」后，数组最大元素已在正确位置，接下来只需排序剩余 (n - 1) 个元素。
同理，对剩余 (n - 1) 个元素执行「冒泡」，可将第二大元素交换至正确位置，因而待排序元素只剩 (n - 2) 个。
以此类推…… 循环 (n - 1) 轮「冒泡」，即可完成整个数组的排序。

C++实现

/* 冒泡排序 */
void bubbleSort(vector<int>& nums) {
    // 外循环：待排序元素数量为 n-1, n-2, ..., 1
    for (int i = nums.size() - 1; i > 0; i--) {
        // 内循环：冒泡操作
        for (int j = 0; j < i; j++) {
            if (nums[j] > nums[j + 1]) {
                // 交换 nums[j] 与 nums[j + 1]
                // 这里使用了 std::swap() 函数
                swap(nums[j], nums[j + 1]);
            }
        }
    }
}

python 实现

""" 冒泡排序 """
def bubble_sort(nums):
    n = len(nums)
    # 外循环：待排序元素数量为 n-1, n-2, ..., 1
    for i in range(n - 1, 0, -1):
        # 内循环：冒泡操作
        for j in range(i):
            if nums[j] > nums[j + 1]:
                # 交换 nums[j] 与 nums[j + 1]
                nums[j], nums[j + 1] = nums[j + 1], nums[j]

算法特性

时间复杂度 (O(n^2)) ：各轮「冒泡」遍历的数组长度为 (n - 1) , (n - 2) , (\cdots) , (2) , (1) 次，求和为 (\frac{(n - 1) n}{2}) ，因此使用 (O(n^2)) 时间。

空间复杂度 (O(1)) ：指针 (i) , (j) 使用常数大小的额外空间。

原地排序：指针变量仅使用常数大小额外空间。

稳定排序：不交换相等元素。

自适应排序：引入 flag 优化后（见下文），最佳时间复杂度为 (O(N)) 。

效率优化

我们发现，若在某轮「冒泡」中未执行任何交换操作，则说明数组已经完成排序，可直接返回结果。考虑可以增加一个标志位 flag 来监听该情况，若出现则直接返回。

优化后，冒泡排序的最差和平均时间复杂度仍为 (O(n^2)) ；而在输入数组 已排序 时，达到 最佳时间复杂度 (O(n)) 。

C++

/* 冒泡排序（标志优化）*/
void bubbleSortWithFlag(vector<int>& nums) {
    // 外循环：待排序元素数量为 n-1, n-2, ..., 1
    for (int i = nums.size() - 1; i > 0; i--) {
        bool flag = false; // 初始化标志位
        // 内循环：冒泡操作
        for (int j = 0; j < i; j++) {
            if (nums[j] > nums[j + 1]) {
                // 交换 nums[j] 与 nums[j + 1]
                // 这里使用了 std::swap() 函数
                swap(nums[j], nums[j + 1]);
                flag = true;  // 记录交换元素
            }
        }
        if (!flag) break;     // 此轮冒泡未交换任何元素，直接跳出
    }
}

Python

""" 冒泡排序（标志优化） """
def bubble_sort_with_flag(nums):
    n = len(nums)
    # 外循环：待排序元素数量为 n-1, n-2, ..., 1
    for i in range(n - 1, 0, -1):
        flag = False  # 初始化标志位
        # 内循环：冒泡操作
        for j in range(i):
            if nums[j] > nums[j + 1]:
                # 交换 nums[j] 与 nums[j + 1]
                nums[j], nums[j + 1] = nums[j + 1], nums[j]
                flag = True  # 记录交换元素
        if not flag:
            break            # 此轮冒泡未交换任何元素，直接跳出

插入排序

「插入排序 Insertion Sort」是一种基于 数组插入操作 的排序算法。

「插入操作」原理：选定某个待排序元素为基准数 base，将 base 与其左侧已排序区间元素依次对比大小，并插入到正确位置。

回忆数组插入操作，我们需要将从目标索引到 base 之间的所有元素向右移动一位，然后再将 base 赋值给目标索引。

插入操作:

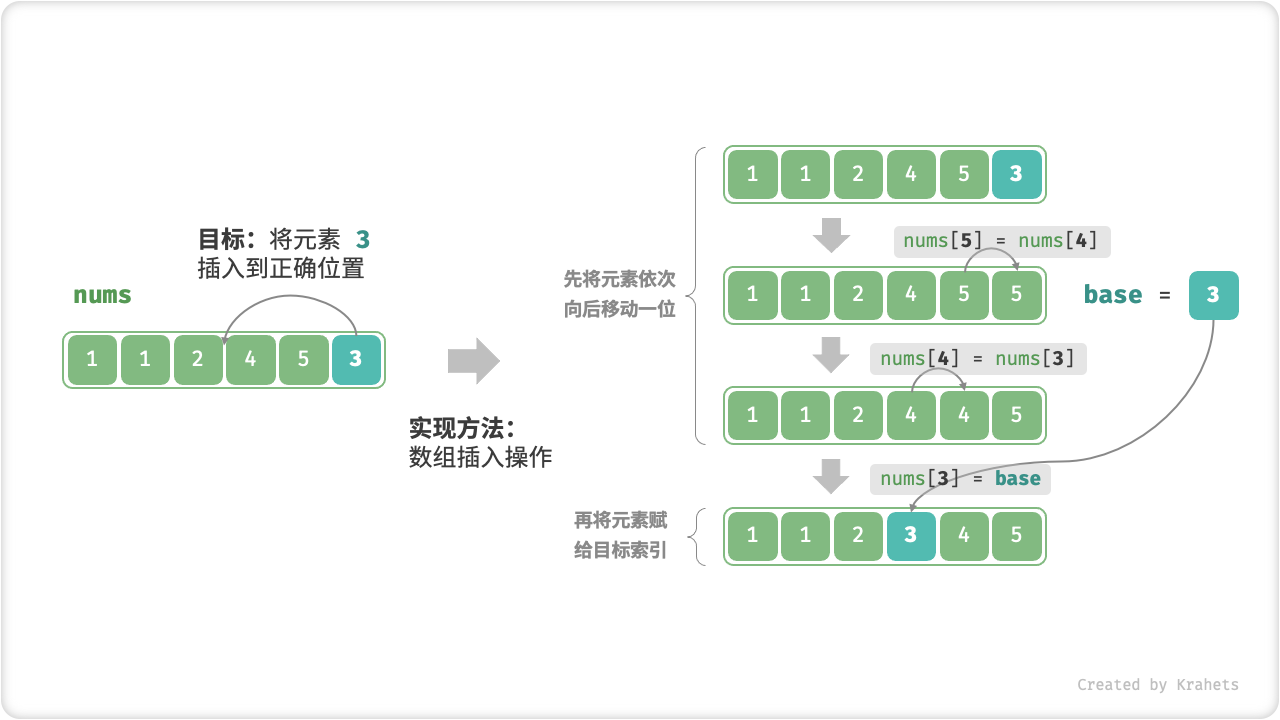
算法流程

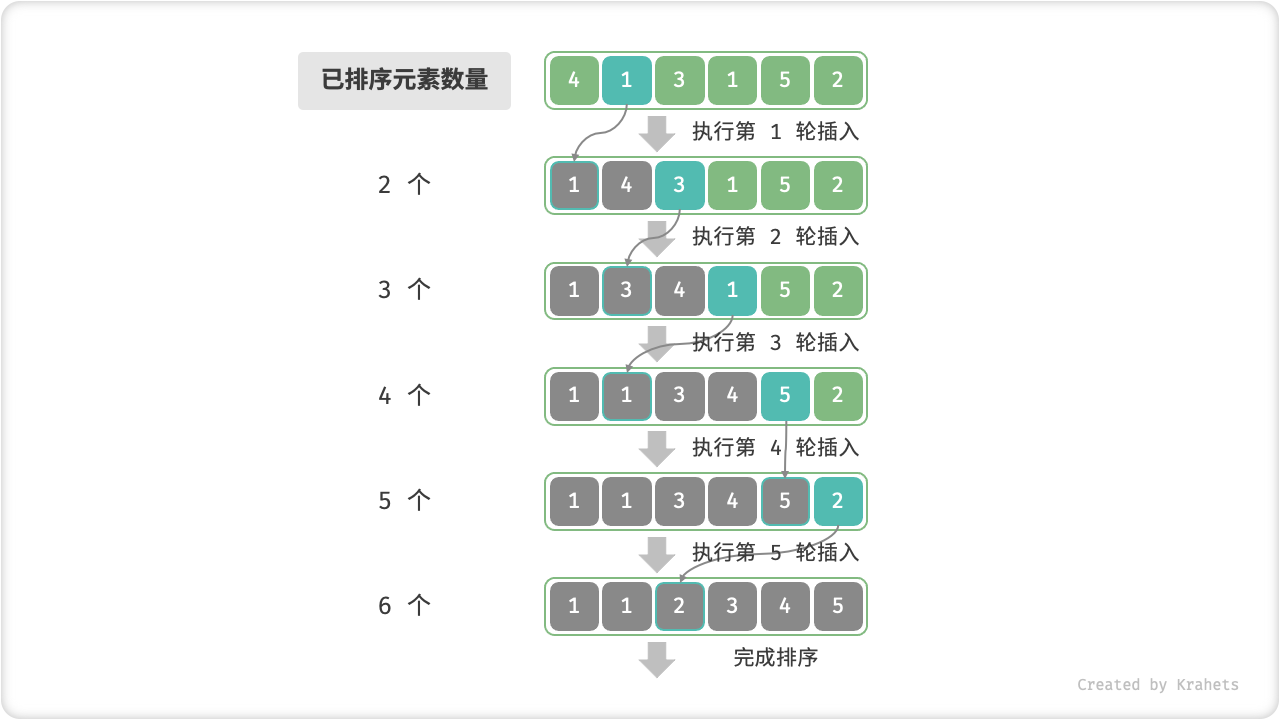
第 1 轮先选取数组的 第 2 个元素 为 base ，执行「插入操作」后，数组前 2 个元素已完成排序。
第 2 轮选取 第 3 个元素 为 base ，执行「插入操作」后，数组前 3 个元素已完成排序。
以此类推……最后一轮选取 数组尾元素 为 base ，执行「插入操作」后，所有元素已完成排序。

插入排序流程

C++

/* 插入排序 */
void insertionSort(vector<int>& nums) {
    // 外循环：base = nums[1], nums[2], ..., nums[n-1]
    for (int i = 1; i < nums.size(); i++) {
        int base = nums[i], j = i - 1;
        // 内循环：将 base 插入到左边的正确位置
        while (j >= 0 && nums[j] > base) {
            nums[j + 1] = nums[j];  // 1. 将 nums[j] 向右移动一位
            j--;
        }
        nums[j + 1] = base;         // 2. 将 base 赋值到正确位置
    }
}